In continuing the game theory series, in this post I will explain one of the most interesting tools from game theory: mixed strategy equilibrium.
To follow along, click the link below to order my Mixed Strategy Equilibrium Excel Template for just $19.

FREE VIDEO TRAINING FOR INNOVATORS
Over 100 Slides Free and Downloadable as a PDF
To view my other posts on game theory, see the list below:
Game Theory Post 1: Game Theory Basics – Nash Equilibrium
Game Theory Post 2: Location Theory – Hotelling’s Game
Game Theory Post 3: Price Matching (Bertrand Competition)
Game Theory Post 4: JC Penny (Price Discrimination)
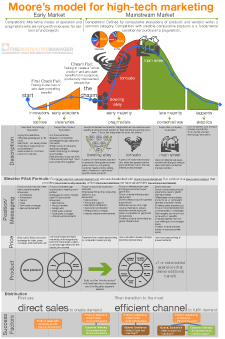
In the examples I’ve used so far, each case illustrated a clear dominant strategy and single Nash equilibrium. But in the real world, this isn’t always the case.
For example, let’s say you’re married and it’s Saturday night and you both want to go out to dinner but your favorite restaurant is Red Lobster and your spouse’s favorite restaurant is Outback. You’re a seafood lover and your spouse is a steak lover. Every time you go out to eat it’s the same argument about where you go. How do you resolve the impasse?
If you’re like many couples, you either “take one for the team” and go with their favorite or your spouse “takes one for the team” and goes for your favorite. But how can we explain this result using game theory?
The answer is to follow these very specific steps:
Step 1: Define the Players
In every game or multi-person interaction, you will have multiple players. The first step to constructing a game theory analysis is to write down the names of the players involved. For simplicity, it’s best to keep the number of players down to just two. Adding more players than two becomes extremely complicated so if your game has more than two players, try to group the players into two broad groups with similar goals.
In continuing the example above, all we have is you and your spouse. To make it easy to keep track of, let’s assume “You” are Mary and “Your spouse” is John. So we list them below:
- You –> Mary
- Your spouse –> John
Simple right? Now on to step two…
Step 2: List the Most Relevant Choices Available to Each Player
This part is pretty simple as well. All we do is take each player and list the choices available to each player. To do this I’ll simply list the two choices for each player in our example.
- Mary
- Red Lobster
- Outback
- John
- Outback
- Red Lobster
Even though I put the choices in order of preference in the list above, putting them in order is not necessary for the analysis. I just put them in order so I could remember which person liked which restaurant better.
Okay, now that we have the players and the choices available to each player listed, there are just a couple more steps before we can start the analysis.
Step 3: Create The Scenarios Matrix
Most people who explain game theory (college professors, etc.) skip this step and jump straight to figuring out the payoff matrix. I’ve found that to be a mistake because often the most challenging part of game theory is simply creating an accurate payoff matrix. By creating a scenarios matrix first, we make it easy to create a payoff matrix.
So what is a scenarios matrix?
A scenarios matrix shows the players and list of choices available to the players in a table or matrix format. The cells inside the matrix represent the specific scenarios that can play out. To setup a scenarios matrix simply take the player names and choices available to each player and list them in a table like below:
Now with the scenarios matrix setup, it’s helpful to think through and write out each scenario within each blank cell. For example, if “Mary” chose “Red Lobster” and “John” chose “Red Lobster” as well (in other words they decide to go to Red Lobster together), then the scenario to write in the first blank cell to the right of “Mary” and “Red Lobster” and underneath “John” and “Red Lobster” would be “Mary and John both choose to go to Red Lobster.”
If you do this for all blank cells, you get the following completed scenarios matrix:
 The great part of having a scenarios matrix is it illuminates all the possible choice combinations available and lets you think through each of them one-by-one. In many cases, this step turns out being the most valuable step in the process. But there are a few more steps before we reach the conclusion of the analysis.
The great part of having a scenarios matrix is it illuminates all the possible choice combinations available and lets you think through each of them one-by-one. In many cases, this step turns out being the most valuable step in the process. But there are a few more steps before we reach the conclusion of the analysis.
Step 4: List How Much Each Player Values Each Choice
This is the step that is usually the most challenging to figure out with a reasonable level of accuracy. But there are a few ways to do it that are relatively easy and straightforward. In our simple example, we can just ask Mary and John in a survey to rate each scenario on a scale of 0-10. For example, below is a survey we could create and ask both of them to answer:
- It’s Friday night and you and your spouse are trying to decide where to go out for dinner. Suppose only the four scenarios below were the set of possible things you could do. Please rate each scenario on a scale of 0-10 how much fun you will have if that scenario played out (10 being the most fun possible, 0 being no fun at all).
- You and your spouse both go to Red Lobster
- You and your spouse both go to Outback
- You choose to go to Red Lobster alone and your spouse chooses to go to Outback alone
- You choose to go to Outback alone and your spouse chooses to go to Red Lobster alone
Now that we have a survey created, let’s ask Mary and John to fill it out. Suppose the following is how they answer:
- Mary’s response:
- You and your spouse both go to Red Lobster –> 9
- You and your spouse both go to Outback –> 6
- You choose to go to Red Lobster alone and your spouse chooses to go to Outback alone –> 1
- You choose to go to Outback alone and your spouse chooses to go to Red Lobster alone –> 0
- John’s response:
- You and your spouse both go to Red Lobster –> 5
- You and your spouse both go to Outback –> 10
- You choose to go to Red Lobster alone and your spouse chooses to go to Outback alone –> 0
- You choose to go to Outback alone and your spouse chooses to go to Red Lobster alone –> 2
Now all we need to do is list these values in a payoff matrix such as the one below. To make it easy to keep track of the payoffs for each I’ve color coded the payoff values to correspond with either Mary or John. All we need to do is enter the values for each cell following the logic in the diagram below:
Once we do this for all the open payoff cells, we get the following:
Step 5: Find the Pure Strategy Nash Equilibrium
Now that we have the payoff matrix complete, the next step is to find the Nash equilibrium. Here it is important to point out that there are two kinds of strategies, pure strategies where the payoff of a choice is always better than the payoff of the other choice. That’s the kind of payoff I’ve discussed in my previous posts on game theory. But when one choice isn’t always better than the other then it’s called a mixed strategy which means that you tend to mix between each choice depending on the timing and circumstances.
Let’s analyze Mary’s options first. Mary can either choose Red Lobster or Outback. If she chooses Red Lobster, depending on what John chooses, her payoff will be either 1 or 9. If she chooses Outback, her payoff will be either 0 or 6. For Mary this poses a bit of a dilemma because if John chooses to go to Outback, Mary will choose to go to Outback as well because a payoff of 6 is better than a payoff of 1. However if John chooses to go to Red Lobster, then Mary will choose to go to Red Lobster as well because a payoff of 9 is better than a payoff of 0. The summary is that even though Mary prefers Red Lobster over Outback, she actually prefers spending dinner with John more than she prefers getting her top restaurant choice.
From John’s perspective it’s basically the same issue. If he chooses to go to Red Lobster his payoff is either going to be 0 or 5 and if he chooses to go to Outback, his payoff is either going to be 2 or 10. This simply means there is no pure strategy equilibrium for either Mary or John but that they both prefer going to dinner together versus going to dinner alone. Hence there are two pure strategy equilibria – they either both go to Red Lobster or they both go to Outback.

PSE stands for Pure Strategy Equilibrium
Okay that’s simple enough. But another question arises: how should Mary decide when to “take one for the team” by choosing Outback instead of Red Lobster and conversely how should John decide when to “take one for the team” by choosing Red Lobster instead of Outback?
Turns out there is a mathematical way to find out.
Step 6: Find the Probability of a Player Making A Certain Choice
From a game theory perspective, this is the step where most people get confused. I know I was when I was first exposed to mixed strategies. To help avoid confusion, before diving straight into setting up and performing the calculations, I want to talk through John and Mary’s story a little more in a way that hopefully helps frame why we’ll setup the calculations in the first place.
First of all its important to note that we are trying to help Mary create a framework for deciding between two options: choosing Red Lobster and choosing Outback. We’ve already determined that Mary only gets meaningful utility from going with John so it’s not really worth it to her to go to Red Lobster alone. Her optimal scenario is to go to Red Lobster with John every time. But we know that’s not possible since John prefers Outback and his optimal scenario is to go to Outback with Mary every time.
Given their situation, there are two general approaches they could take to deciding when to go to Red Lobster (Mary’s first choice) or when to go to Outback (John’s first choice), one is to follow a pattern, another is to decide at random.
Following a Pattern versus Choosing at Random
Let’s suppose John and Mary agree that they will trade off each month on who chooses where to go. For example, Mary could say to John that every odd month he gets to choose and every even month she gets to choose. This arrangement provides a very clear and easy to understand pattern to follow. Sounds reasonable and fair but there’s one critical problem with it: Mary’s decision-making criteria is exposed and now subject to manipulation by John.
Let’s suppose John and Mary have a great relationship in general but they always seem to argue about this particular point and both Mary and John are quite clever at getting their way on this issue. If they follow the pattern that Mary suggests above, John can now employ various strategies to distort that pattern in his favor. For example, in January Mary agrees to go to Outback with John because January is an odd month. This was Mary’s suggestion. But in February, an even month when Mary gets to choose, John unfortunately gets ill and it turns out they won’t be able to go after all. Illnesses happen occasionally so it’s reasonable to give John a pass on going to Red Lobster in February.
March roles around and since it’s an odd month, John gets to choose – they both go to Outback, again.
April comes and finally Mary gets to choose where they go. They set aside a night in their busy schedule but despite the planning John forgot to mention him and his friends had been planning a get together to watch a basketball game and he won’t be able to make it.
Mary catches on. She can tell she’s being manipulated by John who is using her own suggested pattern against her.
This is the problem with making decisions by following a predictable pattern – competitors will exploit that pattern and use it against you!
What’s the solution? It’s simple: to have the other player think your decisions are made randomly. This is the best solution for game theory strategy that involves situations that repeat themselves (i.e. “repeated games”) and that have multiple Nash equilibrium.
John and Mary’s case is kind of a silly example of this but think about it in a variety of competitive settings such as business or war and you quickly see how important this concept is.
Imagine if you were running a retail store and every year for Black Friday you decide to mark all toys down 30%. This is a simple way for you to manage Black Friday and you’ve done it for several years in a row now.
Now consider what your competition across the street, another retailer who also sells toys, is thinking. They’ve started to notice this pattern of yours and they want to figure out a way to exploit it so they can drive more sales to their store. So the next Black Friday they decide to mark things down 35% and tout that all their sales are better than yours. All the customers flock to your competitor and from then on out you decide to be much more creative in your Black Friday sale initiatives.
In war this concept is even more crucial. Some of the most important battles in history were turned in favor of the side that held “the element of surprise.” The Battle of Incheon during the Korean War is a classic example of this.
Another example is the rock, paper, scissors game. If your opponent knows that you tend to alternate between rock and paper, they’ll choose to alternate between paper and rock and defeat you.
Or think about why football players and coaches watch so much game footage of their opponents. The hope is to discover and learn the opponents patterns of play calling and execution.
In short, following a pattern as a decision framework can have negative consequences if that pattern is discovered by your opponent. Hence the advantage of being perceived to make decisions randomly.
Just because your strategy is perceived as random doesn’t mean it’s actually random. Your goal is to give your opponent the impression that you make decisions randomly, not that you actually should make them randomly. What I mean by that is by determining beforehand the probabilities you should pick a strategy with, you can follow a pattern of randomness. Following a pattern of randomness, using probabilities as your guide, is much more difficult to exploit than following a simple pattern because you can always skew the probabilities whenever your opponent seems to start catching on. Once you’ve confused them then you can revert back to making choices based on your optimal probability mix.
Getting back to our example, to determine these probabilities, lets first say that Mary will choose Red Lobster with probability p. In other words, we’ll let p represent Mary’s likelihood of choosing Red Lobster. Since her only other choice is Outback, we can also say that her probability of choosing Outback is equal to 1-p. Let’s also say that John will choose Red Lobster with probability q and Outback with probability 1-q. John’s probabilities are incredibly important to Mary because they impact her actual payoffs associated with each choice.

For example, let’s say Mary would like to know the probability of John choosing Red Lobster versus Outback. Since he’s either going to choose one or the other, if Mary knows how likely John is to choose one or the other then she can properly calculate her expected payoffs.
Let’s suppose Mary chose Red Lobster. If she chooses Red Lobster there are two possible scenarios – John chooses Red Lobster and Mary gets a 9 payoff or John chooses Outback and Mary gets a 1 payoff. Since John mixes between Red Lobster and Outback according to the probabilities q or 1-q, Mary can create an equation that represents her average expected payoff for choosing Red Lobster by multiplying her payoff for each scenario by John’s probability for each scenario and adding them together. In this case, the first scenario is that Mary chooses Red Lobster and John chooses Red Lobster with probability q. Mary’s actual payoff then is 9q. The second scenario is Mary chooses Red Lobster and John chooses Outback with probability 1-q. Mary’s actual payoff in that scenario is 1(1-q). If you add those two together you get 9q+1(1-q) which is the total expected payoff for Mary if she chooses Red Lobster.

As shown above the same can be done if Mary decides to choose Outback. In that case her expected payoff is 0q+6(1-q).
Now for the interesting part…
For Mary to truly seem like she’s making decisions randomly, she needs to appear to John as if she doesn’t care if she goes to Red Lobster or Outback. In other words, she needs to seem like she’s indifferent between the two options. The only way she would be indifferent between the two options is if the payoffs for both were equivalent. Therefore the next step for Mary is to set her two payoffs equal to each other and solve for John’s optimal probability!
 In the calculations to the left all I did was set Mary’s two payoffs equal to each other and using Algebra was able to solve for q – John’s optimal probability. I was able to check my work using Math Papa’s Algebra Calculator.
In the calculations to the left all I did was set Mary’s two payoffs equal to each other and using Algebra was able to solve for q – John’s optimal probability. I was able to check my work using Math Papa’s Algebra Calculator.
The result of this calculation is that John would choose Red Lobster 36% of the time and Outback 64% of the time. What this basically means is that if John is playing the game smartly by seeming to choose Red Lobster or Outback at random then he would mix between the two according to those probabilities. He would choose Red Lobster 36% of the time and Outback 64% of the time.
In John’s case the process is the same if he were to analyze Mary’s strategy. If we put ourselves in John’s situation we then calculate his payoffs as a function of Mary’s decision below.

Note that John’s payoff for choosing Red Lobster is expressed as 5p+0(1-p) and his payoff for choosing Outback is 2p+10(1-p). We then set those payoffs equal to each other and solve for Mary’s optimal probability mix. See below for that calculation:

The result of this is that Mary would choose Red Lobster 77% of the time and Outback 23% of the time.
Now that we know each players optimal mixing strategy we can create the framework for Mary to make her decision. In game theory we call this a “reaction function.”
Step 7: Determine the Optimal Response By Creating A Reaction Function
A reaction function is simply a formula that calculates the optimum response given another players actions. For example, in this case, since there is no pure strategy and we know that John will be mixing between choosing Red Lobster and Outback, our objective is to give Mary a framework for her to make an optimum choice depending on how often John chooses Red Lobster (q). To do that we simply use the two equations we found that calculate Mary’s expected utility given John’s choice of q.
Mathematically these are expressed as the following:
Mutility-Outback(q) = 0q+6(1-q)
Mutility-RedLobster(q) = 9q+1(1-q)
With these equations we then create the following reaction function table and graph.


What this reaction function does is tell Mary what her optimal choice is given how often John chooses Red Lobster. Said another way, let’s say Mary has been keeping detailed track of each choice John makes every month (or week) when they decide to go out to dinner. Let’s suppose she’s seen the following pattern:
Week 1: John chooses Red Lobster
Week 2: John chooses Outback
Week 3 John chooses Red Lobster
This essentially means that John has chosen Red Lobster 67% of the time. According to the graph above she should choose Red Lobster as well because that choice will give her an approximate utility of 6.
However let’s suppose she noticed a different pattern such as the following:
Week 1: John chooses Outback
Week 2: John chooses Outback
Week 3 John chooses Outback
This essentially means John has chosen Red Lobster 0% of the time (i.e. refused Red Lobster) and given this pattern Mary’s optimal choice is Outback according to her reaction function.
Another way to express this is in terms of Mary’s choice of p. Below is a graph that illustrates this:

All this graph is telling us is that whenever John chooses Red Lobster less than 37% of the time (q), Mary should choose Red Lobster 0% of the time (p). And whenever John chooses Red Lobster more than 37% of the time (q), Mary should choose Red Lobster 100% of the time (p).
Note that the same analysis should be done for John as well because that’s how we’ll find out where all of this will eventually settle out in what’s called the Mixed Strategy Nash Equilibrium.
For John here is the analysis:
Jutility-Outback(p) = 0q+6(1-q)
Jutility-RedLobster(p) = 9q+1(1-q)
With these equations we then create the following reaction function table and graph.


The interpretation is the same for John though with different thresholds. Note that the above graph shows that John should choose Outback unless Mary is choosing Red Lobster more than ~76% of the time. If John actually follows through with these reaction functions, it’s safe to say that he’s a pretty stubborn guy!
To follow along, click the link below to order my Mixed Strategy Equilibrium Excel Template for just $19.
The alternative graph for John is displayed below:

Now that we have both of these reaction functions done we can calculate the mixed strategy Nash Equilibrium for this situation. To do that all we need to do is combine the data from the two best response functions into one graph and find the intersect of the two functions. See below:

And there it is. According to this diagram the Mixed Strategy Nash Equilibrium is that John will choose Red Lobster 36% of the time (and Outback 64% of the time) while Mary will choose Red Lobster 77% of the time (and Outback 23% of the time). Note that PSE stands for Pure Strategy Equilibrium.










.jpg?resize=640%2C426&ssl=1)





And she will 100% leave your ass, for taking so long to make decisions. But seriously, thanks for this great piece.